摘要：用GPS可以精確地測定三維坐標X，Y，Z和大地高差H,利用GPS測得的大地高結合現有的水準資料可求出具有正常高h的GPS點的高程異常，再用數字擬合法，可計算出其它GPS點的高程異常和正常高。本文結合具體實例，介紹和分析利用GPS測定地面點高程的方法和達到的精度。

　　關鍵詞：GPS大地高，高程異常，高程擬合，數學模型

　　Abstract: using GPS can measure exactly 3 d coordinate X, Y, Z and the earth difference H, using GPS measurement of the earth with high level of existing data for a normal high H GPS point of abnormal height, garnish with digital intends to legal, may be calculated other GPS point of abnormal height and normal high. This paper based on some examples, introduction and analysis to determine the ground using GPS point of methods and achieve elevation accuracy.

　　Keywords: GPS the earth is high, the abnormal height, elevation fitting, the mathematical model

　　中圖分類號：P228.4 文獻標識碼：A 文章編號：

　　0 引言

　　由GPS相對定位得到的三維基線向量,通過GPS網平差,可以得到高精度的大地高差。如果網中一點或多點具有精確的WGS-84大地坐標的大地高程,則在GPS網平差后,可求得GPS點的WGS-84大地高程。實際應用中,地面點的高程采用正常高系統,正常高Hr是地面點延鉛垂線至似大地水準面的距離。是通過水準測量的方法來確定的,這就需要確定大地高與正常高的關系。似大地水準面與參考橢球面間的高差即高程異常,有Hr=H84-ζ,其中Hr為正高。高程擬合方法的基本思路是:在GPS網中聯測一些水準點(要求這些點分布均勻、密度充分),再利用這些點上的正常高和大地擬合高求出它們的高程異常值,再據這些點上的高程異常值與坐標的關系,用最小二乘方法擬合測區的似大地水準面,利用擬合的似大地水準面內插入其它GPS點的高程異常,從而求出各個未知點的正常高

　　1 GPS測定地面點高程的原理和擬合法數學模型

　　我國高程系統采用的是正常高系統，在工程建設中我們常常用到的地面點高程是地面點到大地水準面的距離，即正常高h，而GPS測定的是地球地心直角坐標系中的基線向量三維坐標差。經過GPS網三維平差后，可獲得GPS點的大地高H,因此地面兩點的正常高之差Δh與大地高之差ΔH的關系為：

　　Δh=ΔH-Δζ Δζ為似大地水準面高之差，即兩點高程異之差。

　　上式中的ΔH可由GPS相位測量精確測定，若要獲得地面兩點正常高之差Δh，首先要求解出Δζ，因此求解高程異常ζ是GPS測定高程的主要問題。

　　由上式可知，GPS網三維最小約束平差后可得到各點大地高Hi，如果我們在GPS網中進行一些水準測量或聯測部分水準高程點，那么就可得到該點的正常高hi,求改點的高程異常ζi 有公式：ζi=Hi-hi

　　若把GPS和水準測量共測點所得到的ζi為已知，再用數學模型擬合其它點高程異常，從而可求得其它點的正常高。

　　1.1曲線擬合

　　當GPS點按線狀布設時,我們可以根據水準重合點的平面坐標和高程異常,擬合出線方向上的似大地水準面曲線,解求插值點的高程異常。若將坐標系轉換成x與測線方向重合,y與測線方向垂直,則設ζ和x間存在下述函數關系:ζm(x0)0=a0+a1 x i+a2 x i2+…am xim;在已知點處的高差Ri=ζm(xi)-ζi;在∑Ri2=min條件下解各ai,繼而求出各點的Hr。當測線長、已知點多、ζ變化大時,按∑Ri2=min解求的ai誤差會增大,故通常總采取分段計算。這樣使曲線在分段點下連續,也影響擬合精度,故采用三次樣條法來擬合。

　　1.2曲面擬合

　　當GPS點布成一定區域面時,可采用數學曲面擬合求待定點的正常高。即根據測區中已知點的平面坐標x,y(或大地坐標B,L)和ζ值,用數值擬合法,擬合出測區似大地水準面再內插出待求點的ζ,從而求出待求點的正常高。設測站點的高程異常ζ與坐標x,y間存在以下函數關系:ζi=f(x i,yi)+εi式中:f(xi,yi)為ζ的趨勢值;εi為誤差。選用空間曲面函數:f(xi,yi)=a0+a1xi+a2 yi+a3xi2+a4xiyi+a5yi2+a6xi3+a7xi2yi+a8xiyi2+a9yi3進行擬合,ai為待定參數。于是,有:ζi=a0+a1 xi+a2 yi+a3 xi2+a4 x i yi+a5 yi2 a6 xi3+a7 xi2+a8 x i yi2+a9 yi3+εi (I=1,2,……,m)式中:m是重合點數。當m大于或等于待定參數ai時,可在[ε2]=min的條件下,求出參數ai,進而求出測區內任意插值點的高程異常值。

　　2 測區GPS網高程擬合方法和精度

　　2.1本溪縣測區GPS網

　　本溪縣城區 GPS網主要是為大比例尺測圖解決平面基礎控制。網中由35個點組成，控制面積約25平方公里，我們觀測的同時，又在15個GPS點上施測四等水準，這些點在GPS控制網中基本分布均勻。

　　GPS外業觀測結束后，對觀測數據預處理并組成GPS基線向量。用GPS后處理軟件對GPS網進行三維最小約束平差。以獲得個點的大地高Hi，在由15個水準點的高程值hi，可得到這些點的高程異常ζi。

　　表1

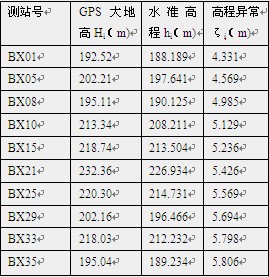
　　由表中可以看出，本測區的內似大地水準面差距ζi由東向西逐漸變大，變化幅度大約為每公里增大5cm，南北變化不是很明顯，并且在測區內沒有發現高程異常大的變動，表明測區內似大地水準面曲線變化比較平緩，但考慮控制面積較大，所以在GPS網周圍和中部選擇了8個水準高程點用作高程控制，進行二次曲面擬合和GPS高程網平差。平差后GPS點高程中誤差最大為±2.1cm,與測區內其它一些四等水準高程比較見表2

　　表2

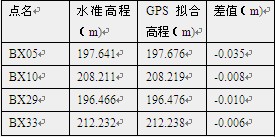
　　3 GPS網高程平差中對水準控制點 的選擇和平差方法

　　運用一次或二次多項式數學模型進行測區大地水準面差距擬合，其可靠性也選擇的高程控制點在網中的分布有較大關系，因此GPS網中選擇合適的高程控制起算點很重要，若不適當，用同級相同個數的高程擬合平差，其結果差別明顯。如在本溪縣城GPS網中，若選擇08,11,16,20四個測站點的水準高程來進行平面擬合(這四個點分布在網的東南部，不覆蓋全網)，平差后高程就增加到±0.028cm。

　　在表1列出的高程異常值中我們還發現，GPS網中點的分布在南北走向上一致，即點的橫坐標值接近時，這些點的高程異常值相差非常小，在相距5公里以內的地面兩點四似大地水準面高之差Δζ小于±3cm，由公式Δh=ΔH-Δζ可得，Δh=ΔH±0.03。因此，在地勢起伏不大的測區，南北一致的GPS點(東西擺動不超過2公里)，直接用GPS測定的高差代替水準高差來推算高程值，精度可達到±3cm。當然，想達到此精度的前提是推算高差的GPS基線向量的質量要可靠，儀器或接收機天線量高要準確。

　　另外，我們施測GPS控制網，一般都是解決平面精度為主，往往要聯測測區外高等級控制點，這樣就會造成GPS網控制面積增大，在GPS高程網平差時最好將那些在測區外的一些點撇開，這樣使高程控制點在小范圍內模擬大地水準面會更可靠，大網也可以使用分區平差的方法。

　　4 結束語

　　上述GPS網高程轉換的精度表明，在地形比較平坦的地區，GPS高程轉換采用曲面擬合法，高程精度可達到±8cm以內，若是局部小范圍的GPS控制網，采用平面或曲面擬合，GPS高程可代替四等水準測量。

　　總之，GPS測量能以很高的精度同時獲取測站點的三維坐標，如果我們只是利用其中的平面位置信息，這無疑是種浪費。通過實例說明，只要采取一定的方法和手段，利用GPS測量中的高程信息解決地面點高程，可獲得較好的效益，可大大減少常規測量的費用和勞動量。

　　參考文獻：

　　[1] 孔祥元，郭際明，劉宗泉編著，大地測量學基礎，武漢大學出版社，2001.

　　[2]徐紹銓，等.GPS測量原理與應用，武漢測繪科技大學出版社，2000

　　[3]徐紹銓.GPS高程擬合系統研究。武漢測繪科技大學學報，1999,12